martes, 8 de noviembre de 2016

PERIODO II



Integral definida

Dada una función f(x) y un intervalo [a,b], la integral definida es igual al área limitada entre la gráfica de f(x), el eje de abscisas, y las rectas verticales x = a y x = b.
gráfica
La integral definida se representa por símbolo integral definida.
∫ es el signo de integración.
a límite inferior de la integración.
b límite superior de la integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.



Propiedades de la integral definida

1. El valor de la integral definida cambia de signo si se permutan los límites de integración.
propiedad de la integral definida
2. Si los límites que integración coinciden, la integral definida vale cero.
propiedad
3. Si c es un punto interior del intervalo [a, b], la integral definida se descompone como una suma de dos integrales extendidas a los intervalos [a, c] y [c, b].
propiedad
4. La integral definida de una suma de funciones es igual a la suma de integrales·
propiedad
5. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
propiedad

Función integral

Sea f(t) una función continua en el intervalo [a, b]. A partir de esta función se define la función integral:
función integral
que depende del límite superior de integración.
Para evitar confusiones cuando se hace referencia a la variable de f, se la llama t, pero si la referencia es a la variable de F, se la llama x.
Geométricamente la función integral, F(x), representa el área del recinto limitado por la curva y = f(t), el eje de abscisas y las rectas t = a y t = x.
gráfica
A la función integral, F(x), también se le llama función de áreas de f en el intervalo [a, b].

Integral indefinida

Integración

Integrar es el proceso recíproco del de derivar, es decir, dada una función f(x), busca aquellas funciones F(x) que al ser derivadas conducen a f(x).
Se dice, entonces, que F(x) es una primitiva o antiderivada de f(x); dicho de otro modo las primitivas de f(x)son las funciones derivables F(x) tales que:
F'(x) = f(x).
Si una función f(x) tiene primitiva, tiene infinitas primitivas, diferenciándose todas ellas en una constante.
[F(x) + C]' = F'(x) + 0 = F'(x) = f(x)

Integral indefinida

Integral indefinida es el conjunto de las infinitas primitivas que puede tener una función.
Se representa por ∫ f(x) dx.
Se lee : integral de f de x diferencial de x.
∫ es el signo de integración.
f(x) es el integrando o función a integrar.
dx es diferencial de x, e indica cuál es la variable de la función que se integra.
C es la constante de integración y puede tomar cualquier valor numérico real.
Si F(x) es una primitiva de f(x) se tiene que:
∫ f(x) dx = F(x) + C
Para comprobar que la primitiva de una función es correcta basta con derivar.

Propiedades de la integral indefinida

1. La integral de una suma de funciones es igual a la suma de las integrales de esas funciones.
∫[f(x) + g(x)] dx =∫ f(x) dx +∫ g(x) dx
2. La integral del producto de una constante por una función es igual a la constante por la integral de la función.
∫ k f(x) dx = k ∫f(x) dx

Ejemplos
    2x dx = x2 + C    		   La intgegral indefinida de 2x respecto a x es x2 + C
    4x3 dx = x4 + C    		   La integral indefinida de 4x3 respecto a x es x4 + C
¿Cómo se trata potencias de x en el denominador, como, por ejemplo,
6

5x4
?
   Primero, conviértalas en forma exponencial; es decir, escriba la expresión con cada término en la forma Axn,  donde A y n son constantes. Por ejemplo, escriba
    6

    5x4
    		como
    6

    5
    		x-4.
Entonces, tome la antiderivada como más arriba; por ejemplo, la antiderivada de esta expreción sería.

SUSTITUCIÓN EN U



Método de sustitución

El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.
integral por sustitución
Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable t, de modo que se obtenga una integral más sencilla.

Pasos para integrar por cambio de variable

integral
1º Se hace el cambio de variable y se diferencia en los dos términos:
cambio
diferenciar
Se despeja u y dx, sutituyendo en la integral:
sustituir en la integral
2º Si la integral resultante es más sencilla, integramos:
integral
3º Se vuelve a la variable inical:
cambio de variable
Ejemplo
integral
cambio de variable
cambia variable
integral
integral
cambie variable
solución


Cambios de variables usuales

1. cambio de variable x = a sen t
2. cambio de variable x = a tg t
3. cambio de variable x = a sec t
4. cambio de variable t = radicando
5. En las funciones racionales de radicales con distintos índices, de un mismo radicando lineal ax + b, el cambio de variable es t elevado al mínimo común múltiplo de los índices.
6. Si racional que una métrica par es par:
cambio de variable
7. Si racional que una métrica par no es par:
cambie variable

Ejemplos

1integral
cambie variable
camero variable
integral
integral
cambie variable
operaciones
cambie variable
operaciones
operaciones
solución
2integral
cambie variable
operaciones
solución
3integral
cambio de variable
operaciones
solución
4integral
cambio de variable
cambio de variable
integral
sangre variable
integral
5integral
cambie variable
integral
integral
cambio de haber cambio de variable
solución
solución
6integra
cambio variable
cambio de variables
sustitución
operaciones
operaciones
operaciones
cambie variable
solución

INTEGRACIÓN POR PARTES

Introducción

Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
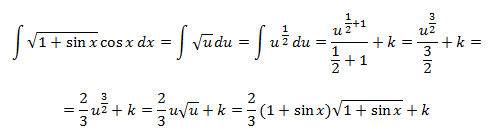
fórmula de integración por partes
Regla mnemotécnica: Un Día Vi Una Vaca MENOS Flaca Vestida De Uniforme (UDV = UV - FVDU)
Aunque se trata de un método simple, hay que aplicarlo correctamente.
Veamos algunos consejos:

Consejos

  • Escoger adecuadamente u y dv:
    Una mala elección puede complicar más el integrando.
    Supongamos que tenemos un producto en el que uno de sus factores es un monomio (por ejemplo x3). Si consideramos dv = x3, entonces, integrando tendremos que v = x4/4. Con lo que hemos aumentado el grado del exponente y esto puede suponer un paso atrás.
    Algo parecido ocurre con las fracciones (como 1/x). Si consideramos dv = 1/x, tendremos v = log|x| y, probablemente, obtendremos una integral más difícil.
    Como norma general, llamaremos u a las potencias y logaritmos; y dv a las exponenciales, fracciones y funciones trigonométricas.
  • No cambiar la elección:
    A veces tenemos que aplicar el método más de una vez para calcular la misma integral. Cuando esto ocurre, al aplicarlo por segunda vez, tenemos que llamar u al resultado dudel paso anterior, y lo mismo para dv. Si no hacemos esto, como escoger una opción u otra supone integrar o derivar, estaremos deshaciendo el paso anterior y no avanzaremos.
  • Integrales cíclicas:
    En ocasiones, tras aplicar dos veces integración por partes, tenemos que despejar la propia integral de la igualdad obtenida para obtenerla.

ejemplos :

  • Integral 1
    ejercicios resueltos integración por partes
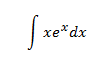    solución 
    Intgramos por partes:
    ejercicios resueltos integración por partes
    Nota: es importante escoger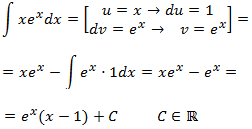
    x=u→dx=du
    ya que de este modo estamos reduciendo el grado del monomio (de 1 a 0). Si por el contrario escogemos
    x=dv→v=x22
    aumentamos el grado (de 1 a 2) y complicamos más la integral ya que el factor de la exponencial se mantiene igual y nos queda la integral
    ∫x22⋅exdx

    Integral 2
    ejercicios resueltos integración por partes
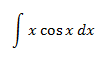    solución 
    Integramos por partes:
    ejercicios resueltos integración por partes
    Nota: al igual que en el ejercicio anterior, como no importa si cos x es u ó dv (ya que obtenemos un sinus), elegimos u = x para disminuir su grado (y así desaparece la x). Si escogemos dv = x, aumentamos su grado: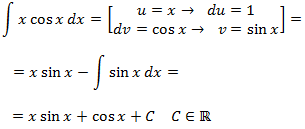
    dv=x→v=x22
  • Integral 10
    ejercicios resueltos integración por partes
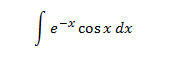    solución 
    En este ejemplo no importa cuáles son los factores u y dv, ya que al integrar y al derivar e-xobtenemos -e-x y al integrar y al derivar cos(x) obtenemos ± sin(x).
    Se trata de una integral cíclica en la que tendremos que aplicar dos veces integración por partes (con la misma elección para no volver al paso anterior) y tendremos que despejar la integral de la expresión obtenida

  • INTEGRAL POR SUSTITUCIÓN TRIGONOMÉTRICA


Las sustituciones que involucran funciones trigonométricas se pueden llevar a cabo en aquellas integrales cuyo integrando contiene una expresión de la forma: 
$\displaystyle {\sqrt{a^{2} - b^{2}x^{2}},\;\sqrt{a^{2} + b^{2}x^{2}}, \sqrt{b^{2}x^{2} - a^{2}}}$ con $a > 0$ y $b>0$ 
La sustitución trigonométrica permite transformar una integral en otra que contiene funciones trigonométricas cuyo proceso de integración es más sencillo. 
Estudiaremos cada uno de los casos como sigue: 
a.
El integrando contiene una función de la forma $\displaystyle {\sqrt{a^{2} - b^{2}x^{2}}}$ con $a>0\; , \;b>0$
Se hace el cambio de variable escribiendo
$\displaystyle {x =\frac{a}{b}\;sen\;\theta,}$donde $\theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[\; y \;x\;\varepsilon \left]\frac{-a}{b}, \frac{a}{b}\right[$
Si $\displaystyle {x =\frac{a}{b}\;sen\;\theta}$ entonces $dx = \frac{a}{b}\;cos\;\theta\;d\theta$
Además: 
$\displaystyle {=\sqrt{a^{2}(1-sen^{2}\theta)} = \sqrt{a^{2}\;cos^{2}\theta} = \vert a\;cos\;\theta\vert = a\;cos\;\theta,}$ pues $a > 0$ y como
$\displaystyle {\theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$ entonces $cos\;\theta>0$ por lo que $\vert a\;cos\;\theta\vert = a\;cos\;\theta$
Luego: $\displaystyle {\sqrt{a^{2} - b^{2}x^{2}} = a\;cos\;\theta}$
Como $\displaystyle {x =\frac{a}{b}\;sen\;\theta}$ entonces $sen\;\theta = \frac{bx}{a} \; y\; \theta = arcsen\left(\frac{bx}{a}\right)$
Para este caso, las otras funciones trigonométricas pueden obtenerse a partir de la figura siguiente:

Ejemplos:

1.$\displaystyle {\int \sqrt{16 - x^{2}}\;dx\; x \varepsilon ]-4,4[}$

Sea $\displaystyle {x = 4\;sen\;\theta}$ con $\displaystyle {\theta\; \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$
$\displaystyle {dx = 4\;cos\;\theta\; d \theta}$
Luego: $\displaystyle {16-x^{2} = 16-16\;sen^{2}\theta = 16\;(1-sen^{2}\theta) = 16\;cos^{2}\theta}$
$\displaystyle {\sqrt{16-x^{2}} = 4\;cos\;\theta}$
Sustituyendo:
$\displaystyle {\int \sqrt{16-x^{2}}\;dx = \int 4\;cos\;\theta \cdot 4\;cos\;\theta\;d\theta = 16\int cos^{2}\theta\;d\theta}$
$\displaystyle {= 16\int \frac{1+cos\;2\theta}{2}\;d\theta = 8\int (1+cos\;2\theta)\;d\theta}$
$\displaystyle {= 8\;(\theta + \frac{1}{2}\;sen\;\theta) + C}$
$\displaystyle {= 8\theta + 4\cdot 2\;sen\;\theta\;cos\;\theta + C}$
$\displaystyle {= 8\theta + 8\;sen\;\theta\;cos\;\theta + C}$
Como $\displaystyle {x = 4\;sen\;\theta}$ entonces $\displaystyle {sen\;\theta = \frac{x}{4}}$ y $\displaystyle {\theta = arcsen\left(\frac{x}{4}\right)}$
Además $\displaystyle {\sqrt{16-x^{2}} = 4\;cos\;\theta}$ por lo que $\displaystyle {cos\;\theta = \frac{\sqrt{16-x^{2}}}{4}}$
Estos resultados también pueden obtenerse a partir de la figura siguiente:

Por último:
$\displaystyle {\int \sqrt{16-x^{2}}\;dx = 8\;\theta + 8\;sen\;\theta\;cos\;\theta + C}$
$\displaystyle {=8\;arcsen\left(\frac{x}{4}\right) + 8\cdot \frac{x}{4}\cdot \frac{\sqrt{16-x^{2}}}{4} + C}$
$\displaystyle {\int \sqrt{16-x^{2}}\;dx = 8\;arcsen\left(\frac{x}{4}\right) + \frac{x\sqrt{16-x^{2}}}{2} + C}$
El integrando contiene una expresión de la forma $\displaystyle {\sqrt{a^{2} + b^{2}x^{2}}}$ con $a>0\; , \;b>0$
Hacemos un cambio de variable escribiendo $\displaystyle {x = \frac{a}{b}\;tan\;\theta,}$ donde $\displaystyle {\theta\; \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$ y$x \varepsilon I\!\!R$
Si $\displaystyle {x = \frac{a}{b}\;tan\;\theta}$ entonces $\displaystyle {dx = \frac{a}{b}\;sec^{2}\theta\;d\theta}$
Además $\displaystyle {\sqrt{a^{2} + b^{2}x^{2}} = \sqrt{a^{2} + b^{2} \cdot \frac{a^{2}}{b^{2}}\;tan^{2}\theta} = \sqrt{a^{2} + a^{2}\;tan^{2}\theta}}$
$\displaystyle {\sqrt{a^{2} + b^{2}x^{2}} = \sqrt{a^{2}(1+tan^{2}\theta )} = \sqrt{a^{2}\;sec^{2}\theta} = \vert a\;sec\;\theta\vert}$
Como ${a>0}$ y $\displaystyle {\theta\; \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$ entonces $\displaystyle {sen\;\theta = \frac{1}{cos\;\theta}}$ es positiva
y por tanto $\displaystyle {\sqrt{a^{2} + b^{2}x^{2}} = a\;sec\;\theta}$
Las otras funciones trigonométricas pueden obtenerse a partir de la siguiente figura:

         Ejemplos:
1.$\displaystyle {\int \frac{dx}{\sqrt{4+x^{2}}}}$
Sea $\displaystyle {x = 2\;tan\;\theta, \theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$
$\displaystyle {dx = 2\;sec^{2}\theta\;d\theta}$
Luego: $\displaystyle {4+x^{2} = 4+4\;tan^{2}\theta = 4(1 + tan^{2}\theta)}$
$\displaystyle {4+x^{2} = 4\;sec^{2}\theta }$
$\displaystyle {\sqrt{4+x^{2}} = \sqrt{4\;sec^{2}\theta} = \vert 2\;sec\;\theta\vert = 2\;sec\;\Theta}$
Sustituyendo
$\displaystyle {\int \frac{dx}{\sqrt{4+x^{2}}} = \int \frac{2\;sec^{2}\theta\;d\theta}{2\;sec\;\theta} = \int sec\;\theta\;d\theta}$
$\displaystyle {ln\;\vert sec\;\theta+ tan\;\theta\vert + C}$
$\displaystyle {\int \frac{dx}{\sqrt{4+x^{2}}} = ln\left\vert \frac{\sqrt{4+x^{2}}}{2} + \frac{x}{2}\right\vert + C}$
2.$\displaystyle {\int \frac{x^{2}\;dx}{\sqrt{x^{2}+6}}}$

Sea $\displaystyle {x = \sqrt{6}\;tan\;\theta, \theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$
$\displaystyle {dx = \sqrt{6}\;sec^{2}\theta\;d\theta}$
Luego: $\displaystyle {x^{2} + 6 = 6\;tan^{2}\theta + 6 = 6(tan^{2}\theta + 1) = 6\;sec^{2}\theta}$
$\displaystyle {\sqrt{x^{2}+6} = \sqrt{6\;sec^{2}\theta} = \sqrt{6}\;sec\;\theta... ...heta>0 si \theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[\right)}$
Sustituyendo
$\displaystyle {\int \frac{x^{2}}{\sqrt{^{2}+6}}\;dx = \int \frac{6\;tan^{2}\the... ...a\;d\theta}{\sqrt{6}\;sec\;\theta} = 6\int tan^{2}\theta\;sec\;\theta\;d\theta}$
$\displaystyle {= 6 \int (sec^{2}\theta - 1)\;sec\;\theta\;d\theta = 6\int(sec^{3} - sec\;\theta)\;d\theta}$
$\displaystyle {= 6 \left[\frac{1}{2}(sec\;\theta\;tan\;\theta) + ln\;\vert sec\... ...eta + tan\;\theta\vert\right] -6\;ln\;\vert sec\;\theta + tan\;\theta\vert + C}$
$\displaystyle {= 3 sec\;\theta\;tan\;\theta - 3\;ln\;\vert sec\;\theta + tan\;\theta\vert + C}$
$\displaystyle {= 3 \cdot \frac{\sqrt{x^{2}+6}}{\sqrt{6}}\cdot \frac{x}{\sqrt{6}... ...;\left\vert\frac{\sqrt{x^{2}+6}}{\sqrt{6}} + \frac{x}{\sqrt{6}}\right\vert + C}$
$\displaystyle {= \frac{x\sqrt{x^{2}+6}}{2} - 3\;ln\;\left\vert\frac{\sqrt{x^{2}+6} + x}{\sqrt{6}}\right\vert + C}$
3.$\displaystyle {\int \frac{x\;dx}{(9+4x^{2})^{\frac{3}{2}}}}$
Sea $\displaystyle {x = \frac{3}{2}\;tan\;\theta, \theta \varepsilon \left]\frac{-\Pi}{2}, \frac{\Pi}{2}\right[}$
$\displaystyle {dx = \frac{3}{2}\;sec^{2}\theta\;d\theta}$
Luego $\displaystyle {9 + 4x^{2} = 9 + 4\cdot \frac{9}{4}\;tan^{2}\theta = 9 + 9\;tan^{2}\theta = 9(1 + tan^{2}\theta)}$
$\displaystyle {9 + 4x^{2} = 9\;sec^{2}\theta}$
$\displaystyle {(9 + 4x^{2})^{\frac{3}{2}} = (9\;sec^{2}\theta)^{\frac{3}{2}} = (9\;sec^{2}\theta)^{3}}$
$\displaystyle {(9 + 4x^{2})^{\frac{3}{2}} = (3\;sec\;\theta)^{3} = 27\;sec^{3}\theta}$
Sustituyendo
$\displaystyle {\int \frac{x\;dx}{(9+4x^{2})^{\frac{3}{2}}} = \int \frac{\frac{3... ...}\theta}\;d\theta = \frac{1}{12} \int \frac{tan\;\theta\;d\theta}{sec\;\theta}}$
$\displaystyle {= \frac{1}{12} \int \frac{\frac{sen\;\theta}{cos\;\theta}}{\frac... ...heta = \frac{1}{12} \int sen\;\theta\;d\theta = \frac{1}{12}(-cos\;\theta) + C}$
Como
$\displaystyle {tan\;\theta = \frac{2x}{3}}$ de la sustitución inicial
Por tanto:
$\displaystyle {\int \frac{x\;dx}{(9+4x^{2})^{\frac{3}{2}}} = \frac{-1}{12} \cdot\frac{3}{\sqrt{9+4x^{2}}} + C}$
$\displaystyle {= \frac{-1}{4\sqrt{9+4x^{2}}} + C }$
c.
El integrando contiene una expresión de la forma $\displaystyle {\sqrt{b^{2}x^{2}- a^{2}}}$ con $a > 0$ y$b>0$
En este caso la sustitución adecuada es:
$\displaystyle {x = \frac{a}{b}\;sec\;\theta,}$donde $\displaystyle {\theta \varepsilon \left]0, \frac{\pi}{2}\right[ \;U\;\left]\pi, \frac{3\pi}{2} \right[}$
y $\displaystyle {x\; \varepsilon \left]-\infty, \frac{-a}{b}\right[ \bigcup \left]\frac{a}{b}, +\infty, \right[, o\; sea \vert x\vert>\frac{a}{b}}$
Si $\displaystyle {x = \frac{a}{b}\;sec\;\theta}$ entonces $\displaystyle {dx = \frac{a}{b}\;sec\;\theta\;tan\;\theta\;d\theta}$
Además $\displaystyle {\sqrt{b^{2}x^{2}-a^{2}} = \sqrt{b^{2}\cdot \frac{a^{2}}{b^{2}}\cdot sec^{2}\theta -a^{2}} = \sqrt{a^{2}(sec^{2}\theta-1)}}$
de donde $\displaystyle {\sqrt{b^{2}x^{2} - a^{2}} = \sqrt{a^{2}\;tan^{2}\theta} = \vert a\;tan\;\theta\vert = a\;tan\;\theta,}$
pues $a > 0$ y $tan\;\theta>0$ para $\theta \varepsilon \left]0, \frac{\pi}{2}\right[ \bigcup \left]\pi, \frac{3\pi}{2}\right[$
Como $\displaystyle {x = \frac{a}{b}\;sec\;\theta}$ entonces $\displaystyle {sec\;\theta = \frac{bx}{a}}$ por lo que $\displaystyle {\theta = arcsen\left(\frac{bx}{a}\right)}$
Utilizando el siguiente triángulo puede obtenerse las otras funciones trigonométricas:

Ejemplos:

1.$\displaystyle {\int \frac{x\;dx}{\sqrt{x^{2}-9}}, \vert x\vert>3}$
 Sea $\displaystyle {x = 3\;sec\;\theta}$
$\displaystyle {dx = 3\;sec\;\theta\;tan\;\theta\;d\theta, \theta \varepsilon \left]0, \frac{\pi}{2}\right[ \bigcup \left]\pi, \frac{3\pi}{2}\right[}$
Luego $\displaystyle {x^{2}-9= 9\;sec^{2}\theta-9 = 9(sec^{2}\theta-1) = 9\;tan^{2}\theta}$
$\displaystyle {\sqrt{x^{2}-9} = \sqrt{9\;tan^{2}\theta} = 3\;tan\;\theta}$
Sustituyendo:
$\displaystyle {\int \frac {x\;dx}{\sqrt{x^{2}-9}} = \int \frac{3\;sec\;\theta \cdot 3\;sec\;\theta\;tan\;\theta\;d\theta}{3\;tan\;\theta}}$
$\displaystyle {= 3\int sec^{2}\theta\;d\theta = 3\;tan\;\theta + C = \sqrt{x^{2}-9}}$
2.$\displaystyle {\int \frac{\sqrt{4x^{2}-1}}{x}\;dx, \vert x\vert>\frac{1}{4}}$
Sea $\displaystyle {x = \frac{1}{2}\;sec\;\theta}$
$\displaystyle {dx = \frac{1}{2}\;sec\;\theta\;tan\;\theta\;d\theta}$
Luego $\displaystyle {4x^{2}-1= 4\cdot\frac{1}{4}\;sec^{2}\theta-1 = sec^{2}\theta-1 = tan^{2}\theta}$
$\displaystyle {\sqrt{4x^{2}-1} = \sqrt{tan^{2}\theta} = tan\;\theta}$
Sustituyendo:
$\displaystyle {\int \frac{\sqrt{4x^{2}-1}}{x}\;dx = \int \frac{tan\;\theta\cdot \frac{1}{2}\;sec\;\theta\;tan\;\theta\;d\theta}{\frac{1}{2}\;sec\;\theta}}$
$\displaystyle {= \int tan^{2}\theta\;d\theta = \int(sec^{2}\theta-1)\;d\theta}$
$\displaystyle {= \int tan\;\theta - \theta + C = \sqrt{4x^{2}-1} - arcsec\;(2x) + C}$
3.$\displaystyle {\int \frac{du}{u^{2}\sqrt{u^{2}-8}}, \vert u\vert>2\sqrt{2}}$
Sea $\displaystyle {u = \sqrt{8}\;sec\;\theta}$
$\displaystyle {du = \sqrt{8}\;sec\;\theta\;tan\;\theta\;d\theta}$
Luego $\displaystyle {u^{2}-8= 8\;sec^{2}\theta-8 = 8(sec^{2}\theta-1) = 8\;tan^{2}\theta}$
$\displaystyle {\sqrt{u^{2}-8} = \sqrt{8\;tan^{2}\theta} = \sqrt{8}\;tan\;\theta}$
Sustituyendo:
$\displaystyle {\int \frac{du}{u^{2}\sqrt{u^{2}-8}} = \int \frac{\sqrt{8}\;sec\;... ...2}\theta\;\sqrt{8}\;tan\;\theta} = \frac{1}{8}\int \frac{d\theta}{sec\;\theta}}$
$\displaystyle {= \frac{1}{8}\int cos\;\theta\;d\theta = \frac{1}{8}\;sen\;\theta + C}$
Como $\displaystyle {sec\;\theta = \frac{u}{\sqrt{8}}}$ puede utilizarse la siguiente figura para determinar$sen\;\theta$

Por último:
$\displaystyle {\int \frac{du}{u^{2}\sqrt{u^{2}-8}} = \frac{1}{8}\;\frac{\sqrt{u^{2}-8}}{u} + C}$

UNIDAD III: APLICACIÓN DE LA INTEGRAL

TEMA 1: ÁREA ENTRE GRÁFICAS

Una forma para hallar el área delimitada entre dos funciones, es utilizando el cálculo integral:


El resultado de esta integral es el área comprendida entre las curvas:
 f(x) y g(x)[<f(x)] y en el intervalo [a,b] .
Ejemplo Si se quiere hallar el área delimitada entre el eje x y la función f(x) = 4 − x2 en el intervalo [ − 2;2], se utiliza la ecuación anterior, en este caso: g(x) = 0 entonces evaluando la integral, se obtiene:

Por lo que se concluye que el área delimitada es 32/3.El volumen encerrado entre dos funciones también puede ser reducido al cálculo de una integral.
Ejemplo de Aplicación 1:
La siguiente grafica representa el área entre funciones explicada anteriormente:
Ejemplo De Aplicacion 2:
La figura 5 hace la función de representar el área desarrollada anteriormente:


TEMA 2: SÓLIDOS DE REVOLUCIÓN


 Los sólidos de revolución son sólidos que se generan al girar una región plana alrededor de un eje. Por ejemplo: el cono es un sólido que resulta al girar un triángulo recto alrededor de uno de sus catetos, el cilindro surge al girar un rectángulo alrededor de uno de sus lados.Si giramos una región del plano alrededor de un eje obtenemos un sólido de revolución. El volumen de este disco de radio R y de anchura ω es:
Volumen del disco = wR2π
Para ver cómo usar el volumen del disco y para calcular el volumen de un sólido de revolución general, se hacen n particiones en la grafica.


Estas divisiones determinan en el sólido n discos cuya suma se aproxima al volumen del mismo. Teniendo en cuenta que el volumen de un disco es wR2π , la suma de Riemann asociada a la partición, y que da un volumen aproximado del sólido es:


Ejemplo 

La región entre  y el eje x se gira alrededor del eje x para generar un sólido. Hallar su volumen.

Región que rota alrededor del eje x
  

2. EXTRACCIÓN DEL RADIO PRINCIPAL:Es claro que el método a utilizar es el método de los discos. Luego, la distancia del segmento r (radio principal) es f, es decir: 
 

3. LIMITES DE INTEGRACIÓN:Estos límites nos lo fueron
Región que rota alrededor del eje x
dados en el enunciado del ejemplo: 


4. FORMULACION DE LA INTEGRAL:Aplicando la expresión correspondiente para volúmenes usando el método del disco tenemos:

  


Por tanto el volumen del sólido es  u3.












Publicado por en 6 comentarios:
Suscribirse a: Entradas (Atom)