"CALCULO INTEGRAL": PERIODO 1 : SUMATORIAS Y ÁREA BAJO UNA GRÁFICA

TEMA 1: "SUMATORIA"

EJERCICIO 1:

EN UN GRUPO DE BACHILLERATO DECIDIERON ORGANIZAR UNA RIFA PARA REUNIR RECURSOS PARA SU FIESTA DE GRADUACIÓN . SE PROPUSIERON DOS PROPUESTAS PARA ORGANIZAR DICHA RIFA, LA PRIMERA CONSISTE EN EMITIR 500 BOLETOS QUE JUEGAN CON DOS NÚMEROS Y SU COSTO ES DE $50.00 CADA UNO. EN EL SEGUNDO CASO CONSISTE EN QUE SE EMITAN SOLO 250 BOLETOS PERO EL COSTO CORRESPONDERÁ AL NUMERO DEL BOLETO, SI EN AMBOS CASOS EL PREMIO ES DE 5,000.00. ¿ QUE TIPO DE RIFA LES CONVENDRÁ MAS ORGANIZAR Y PORQUE?
R= la segunda opción debido a que se gastara menos y se ganara mas

RESPONDE LAS SIGUIENTES PREGUNTAS:

¿Cuales son las ventajas y desventajas de cada propuesta?

R= la primera es mas fácil de vender pero menos ganancias en canvio la segunda es mas difícil pero se obtiene mas ganancia

¿cuanto se obtiene de ganancia en cada caso?

R= 250 y 45000

¿cuanto se obtendría de ganancia si se aumenta al doble el numero de boletos en cada caso?

R= 25,000

¿seria recomendable aumentar el numero de boletos en la segunda propuesta?

R= seria mas conveniente por el precio

Notación Sigma

El operando matemático que nos permite representar sumas de muchos sumandos, n o incluso infinitos sumandos está expresado con la letra griega sigma 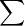$\sum$ (sigma mayúscula, que corresponde a nuesta S de"suma" ). La notación sigma es de la siguiente manera:

$\sum_{i=m}^n x_i = x_m + x_{m+1} + x_{m+2} +\cdots + x_n$

Esto se lee: Sumatorio sobre i, desde m hasta n, de x sub-i.

La variable i es el índice de suma al que se le asigna un valor inicial llamado límite inferior, m. La variable i recorrerá los valores enteros hasta alcanzar el límite superior, n. Necesariamente debe cumplirse que:

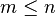
$m \leq n$